Gauss's Law

Gauss's law, a cornerstone of electromagnetism, provides a powerful tool for understanding the relationship between electric fields and electric charges. Formulated by the renowned German mathematician and physicist Carl Friedrich Gauss in the early 19th century, this fundamental principle has had far-reaching implications in various fields of science and technology.

Carl Friedrich Gauss

Delving into the Essence of Gauss's Law

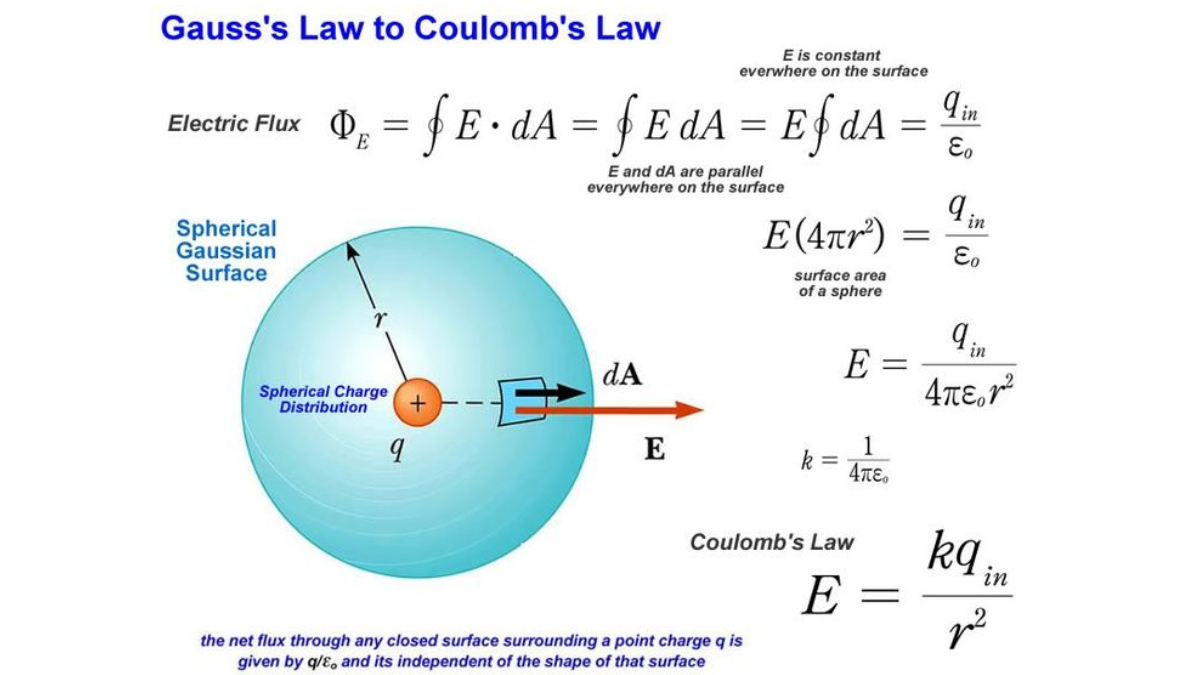
Gauss's law, also known as Gauss's flux theorem, states that the total electric flux through a closed surface is proportional to the net electric charge enclosed by the surface. Mathematically, it can be expressed as:

Φ_E = ∮E·dA = Q_enc/ε₀

where:

Φ_E is the total electric flux through the closed surface
E is the electric field
dA is the infinitesimal element of area
∮ is the integral over the closed surface
Q_enc is the net electric charge enclosed by the surface
ε₀ is the permittivity of free space

The integral in Gauss's law represents the total electric flux passing through the closed surface. The right-hand side of the equation relates this flux to the enclosed charge.

Understanding the Implications of Gauss's Law

Gauss's law has profound implications in various fields of science and technology:

Charge Distribution Analysis: Gauss's law provides a powerful tool for analyzing the distribution of electric charges within a region. By applying Gauss's law to closed surfaces of appropriate shapes, the charge distribution can be determined.
Electric Field Calculation: Gauss's law simplifies the calculation of electric fields in situations where the charge distribution exhibits certain symmetries. For instance, the electric field around a uniformly charged sphere or an infinite charged plane can be easily determined using Gauss's law.
Electromagnetic Applications: Gauss's law plays a crucial role in understanding and analyzing electromagnetic phenomena, including the propagation of electromagnetic waves, the behavior of electric fields in conductors, and the design of various electrical devices.

Applications of Gauss's Law

Gauss's law has found wide-ranging applications in various fields, including:

Physics: Gauss's law is an essential tool in electromagnetism, used to study the behavior of electric fields, charge distributions, and electromagnetic waves.
Engineering: Electrical engineers utilize Gauss's law to analyze and design various electrical devices, such as capacitors, particle accelerators, and electrostatic filters.
Material Science: Gauss's law is employed to study the dielectric properties of materials, where electric dipoles are aligned, influencing their behavior in electric fields.
Geophysics: Gauss's law is used to model the Earth's magnetic field and study its interactions with charged particles in the atmosphere.

Conclusion: Gauss's Law – A Cornerstone of Electromagnetism

Gauss's law, with its elegance and far-reaching implications, stands as a fundamental principle in electromagnetism. Its understanding is essential for comprehending the behavior of electric charges, electric fields, and electromagnetic phenomena. From charge distribution analysis to electromagnetic wave propagation, Gauss's law serves as a powerful tool in unraveling the mysteries of electromagnetism and shaping technological advancements.