
Equation of Continuity
Introduction
What is the Equation of Continuity?
Briefly explain the significance of the Equation of Continuity in fluid dynamics.
Introduce the concept of conservation of mass of fluid flow.
Key Concepts
Fluid Flow and Conservation of Mass
Discuss the basic principles of fluid flow.
Explain how mass is conserved in a closed system.
The Equation of Continuity: An Overview
Present an overview of the Equation of Continuity.
Mention its applications in various fields, such as fluid mechanics, aerodynamics, and hydraulics.
Deriving the Equation of Continuity
The Incompressible Flow Assumption
Explain the incompressible flow assumption and its significance.
Provide examples of when this assumption is applicable.
Cross-Sectional Area and Velocity
Define cross-sectional area and velocity as they relate to fluid flow.
Explain how changes in these parameters affect mass flow.
Deriving the Equation
Present the step-by-step derivation of the Equation of Continuity.
Include mathematical equations and explanations.
Practical Applications
Flow in Pipes and Tubes
Discuss how the Equation of Continuity is used to analyze fluid flow in pipes and tubes.
Provide practical examples and real-world applications.
Aerodynamics and Aviation
Explain how the
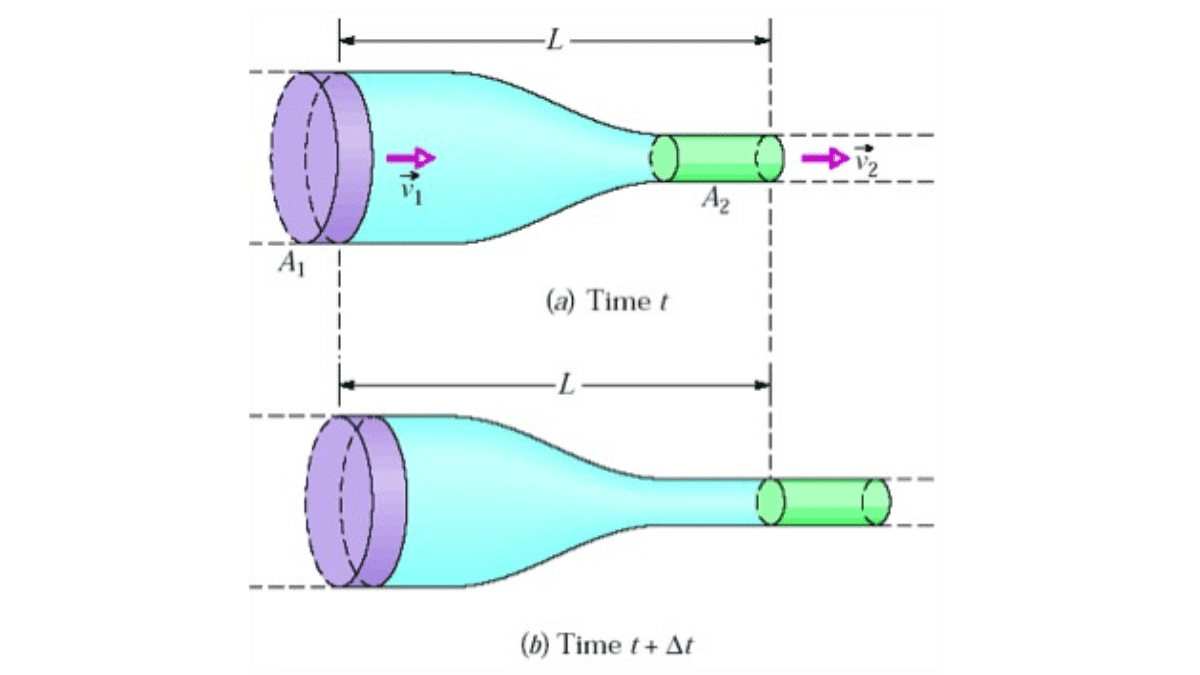
Image of continuity is essential in aviation and aerodynamics.
Describe its role in understanding lift and airspeed in aircraft.
Hydraulics and Fluid Machinery
Discuss the application of the Equation of Continuity in hydraulic systems and fluid machinery.
Provide examples of hydraulic engineering.
Visualizing Fluid Flow
Using Diagrams and Flow Charts
Include diagrams and flow charts that visually represent the Equation of Continuity.
Illustrate the concepts of mass flow and changing cross-sectional areas.
Interactive Animations
Embed interactive animations or simulations that help users understand fluid flow and the Equation of Continuity.