
Bernoulli Equation
Introduction
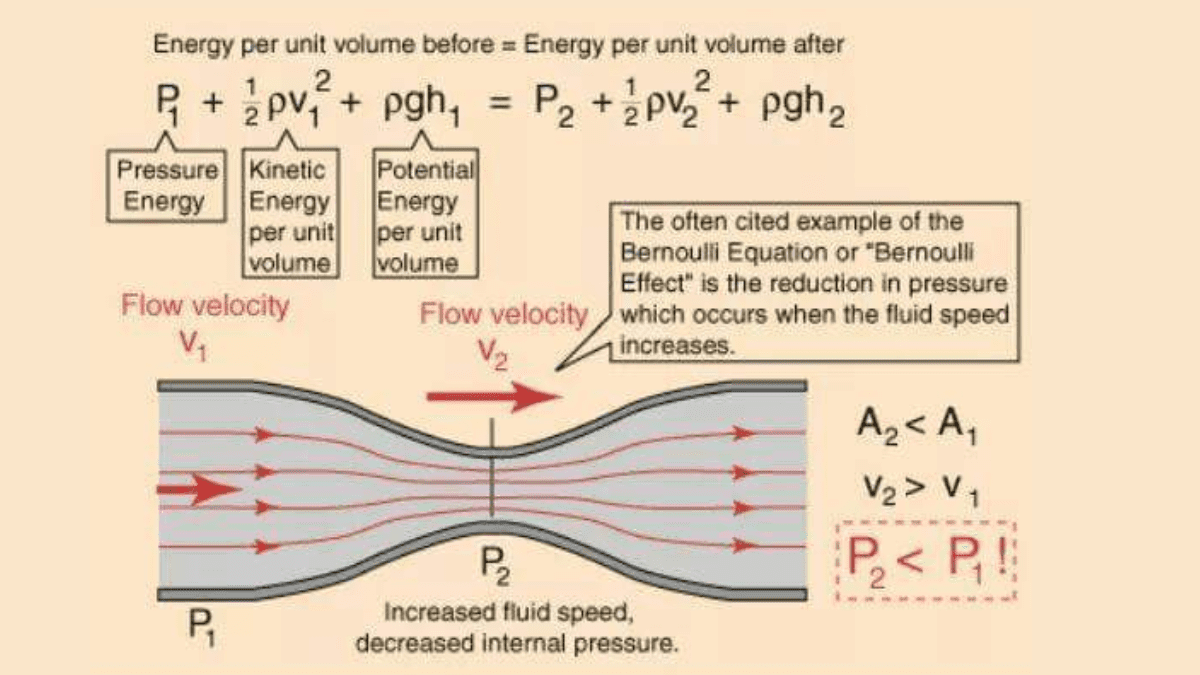
The named after the Swiss scientist Daniel Bernoulli, is a fundamental principle in fluid dynamics that describes the relationship between pressure, velocity, and potential energy in a fluid flow. It is derived from the principle of conservation of energy for a fluid particle as it moves along a streamline.
Key Components
The Bernoulli equation consists of three main components:
1. Kinetic Energy Component
The first component of the Bernoulli equation is the kinetic energy term, which relates the fluid velocity to kinetic energy.
Kinetic Energy Term:
1/2pv2
ρ : The density of the fluid.
v : The velocity of the fluid at a specific point along the streamline.
2. Pressure Component
The second component of the equation represents the pressure energy of the fluid. It takes into account the pressure at the point of interest.
Pressure Term: P
P : The pressure of the fluid at the point of interest.
3. Potential Energy Component
The third component deals with potential energy in the fluid, taking into account the height of the fluid above a reference point.
Potential Energy Term: ρgh
ρ : The density of the fluid.
g : The acceleration due to gravity.
h : The height of the fluid above a reference point.
Bernoulli Equation
When these three components are combined, the Bernoulli equation can be expressed as:
1/2 ρv2+P+ρgh=constant
This equation states that the total energy (sum of kinetic energy, pressure energy, and potential energy) of a fluid particle remains constant along a streamline, provided there are no energy losses due to viscous forces or other external work.
Applications
The Bernoulli equation is commonly used in various applications, such as:
Aerodynamics: Analyzing the flow of air around aircraft wings.
Hydraulics: Understanding the behavior of fluids in pipes, pumps, and valves.
Weather: Describing the atmospheric flow of air.
Medicine: Analyzing blood flow in arteries and veins.
Fluid mechanics: Studying the behavior of fluids in general.
In summary, the Bernoulli equation is a valuable tool for understanding the behavior of fluids in a wide range of practical scenarios, and it provides insights into the interplay of kinetic energy, pressure, and potential energy within a fluid.
Appreciate the creator